This is the presentation I gave at the Wolfram User Conference in 2007, updated for version 8. Part Two is here.
A New Mathematica Programming Style, Part One
Kris Carlson
Author, The Way of Mathematica (forthcoming)
An Historical Perspective on Computer Programming
"The computer revolution is a revolution in the way we think and in the way we express what we think. The essence of this change is the emergence of ... procedural epistemology--the study of the structure of knowledge from an imperative point of view, as opposed to the more declarative point of view taken by classical mathematical subjects. Mathematics provides a framework for dealing precisely with notions of 'what is.' Computation provides a framework for dealing precisely with notions of 'how to.'"
Harold Abelson and Gerald Jay Sussman, The Structure and Interpretation of Computer Programs
Origins of Geometry
Beginnings: Accurately surveying land boundaries
Destiny: Euclid's creation of the first axiomatic science
Origins of Computer Programming
Beginnings: Very abstract notions of computation by Church, Turing, Kleene and others
Destiny: The control of complex processes
The Main Challenges of Modern Science
Genetic Engineering
Taking control of the analog computer program immanent in DNA-RNA-protein
Artificial Intelligence
Reverse-engineering the agencies of intelligence created by evolution and creating new ones
Creating and initially controlling intelligences greater than our own
Nanotechnology
Programming at the atomic and molecular level to control materials
These challenges put the Abelson/Sussman thesis in perspective : It' s all about controlling complex processes
What about "A Theory of Everything?"
A misnomer. If created, which I doubt it will be, it would be nothing more than a theory of the currently known physical microcosm
Note that computer programming cannot be derived from it--but it can be derived from computer programming
Mathematica's Place in History
Mathematica is a scientific synthesis like those of Euclid, Spinoza, Newton, Locke, Lagrange, Hamilton, Darwin, Maxwell, Gibbs, Shannon, and others
"Everything is an expression"--a central unifying syntactic principle like energy in physics or bits in information theory
More Elements of the Mathematica Synthesis
General symbol manipulation program
Pattern matching engine
A variety of programming styles and devices
Axiomatization of lower-level functionality (Table, Map* family, Nest* family, etc.)
Interpret and compile modes
Interface/IDE\--the Front End Notebook
Plethora of built-in functions
Extension to all special functions via Mathematica Functions site
Extensive and growing graphics and visualization capabilities
Effectively unlimited notation synthesis
Equation solving
Numerical analysis/evaluation
Axiomatization of higher-level functionality (CellularAutomata, Manipulate, TuringMachine, etc.)
gridMathematica
Documentation Center
MathWorld
Presentation and documentation formats
webMathematica
Demonstrations site
Curated data/Data paclets
Incipient semantic net (WordData)
What is the goal of programming style?
Help manage ever-increasing complexity
Streamline the human-computer interface from both sides
A New Mathematica Programming Style
First principle: Replace all matchfix single argument function applications f [ arg ] with Prefix function applications f @ arg
Requires some knowledge of the 1000-level Precedence table
Second principle: Replace nested matchfix with Postfix + pure Function
Prefix Functional Syntax
Cleaner and more efficient than matchfix
Use prefix function application, @, for single-argument functions
Matchfix style:
f[ g[ h[ i [j] ] ] ]
Prefix style:
f @ g @ h @ i @ j
First two syntactical problems with list- or matchfix-based language
- Humans have difficulty parsing deeply nested expressions (>3)
- Humans are not regular expression parsers
Basic Benefits of Prefix style
Every pair of brackets we lose makes our expressions easier to read and understand
Every pair of brackets for which we don't have to type or move the cursor saves us time
A Prefix Style Example
Each @ tells us there is no complex nesting for that function, no options or arguments to look for, no brackets to match.
We can focus our attention on the functions that do use matchfix and identify their arguments and options.
There are fewer nested brackets to sort out.
Here's some code from Trott, The Mathematica Guide to Graphics, in matchfix and Prefix styles:
Show[GraphicsArray[
Block[{$DisplayFunction = Identity},
(* display absolute value of 2D Fourier transform *)
ListDensityPlot[Abs[Fourier[Table[1/#[i, j], {i, 256}, {j, 256}]]],
Mesh -> False, ColorFunction -> (Hue[0.8 #]&)]& /@
{GCD, LCM}]]]
Show@GraphicsArray@
Block[{$DisplayFunction = Identity},
(* display absolute value of 2D Fourier transform *)
ListDensityPlot[
Abs@Fourier@Table[1/#[i, j], {i, 256}, {j, 256}],
Mesh -> False, ColorFunction -> (Hue[0.8 #]&)]& /@
{GCD, LCM}]
More Prefix Style Examples
Basic Usages
One argument function definitions:
f[x_] := Sin[x]
f@x_ := Sin@x
One argument functions or assignments:
Log@100^100//N
2.11139*10^66
walk1D3@n_:= NestList[#+Random[Real,{-1,1}]&, Random[Real, {-1,1}],n];
walk1D3@10
{-0.206019, -0.914893, -0.951759, -1.04967, -0.299963, -0.8917, -0.147434, 0.764746, 1.57289, 1.40045, 2.13796}
list5 = Range@10;
Clear@list5;
Histogram@%
Histogram[Null]
Needs@"Combinatorica`"
Multiple one-argument function composition:
f@g@h@i@j@k
Sin[g[h[i[j[k]]]]]
First@Rest@Most@Range@10
Function definitions with lists as argument:
f@{a_, b_, c_}:= n@{a,b,c}
Precedence in Mathematica
The main objection to Prefix is that you have to know operator precedence
However this objection applies to all abbreviated operators (+, *, ^, [[ ]], { }, /@, etc.)
Mathematica is endowed with "a variety of special characters that greatly increase readability and elegance."
FORTRAN (FORmula TRANslation; early and primitive, but elegant), Mathematica (an advanced synthesis):
A conscious effort was made to provide a path of least action or smooth transduction from mathematical notation to code
Further, a significant feature of V6 is the addition of 100 undefined operators to facilitate creating user-defined notations
I submit that if you use Prefix, you will use it more often than the most common abbreviated operators
Precedence directs the order of abbreviated operators' operation
Precedence can be symbolized by parenthetical grouping, such as: a + (b ^ c) versus (a + b) ^ c
The Mathematica reference on precedence in 5.2 was Table A.2.7, now is in tutorial / InputSyntax: Operator Input Forms
It lists all abbreviated operators in tables of decreasing precedence
However, a superior reference can be generated from a little code
There exists an undocumented function, Precedence
Voila:
Precedence@Prefix
640.
It is not Listable, but it should be! Either reset Attributes to Listable or just Map it:
Precedence /@ {Prefix, Factorial}
{640., 610.}
What happened in the previous slide?
Prefix is a little "stickier" than Factorial==@ sticks to n more than ! does--and so we got (IntegerDigits@n)! instead of IntegerDigits[ n! ]
When faced with a few abbreviated operators, map Precedence onto them in the order they present in your expression
a + b * c ^ d - e
Precedence /@ {Plus, Times, Minus, Power}
{310., 400., 480., 590.}
Precedence mnemonics: Think of operator "stickiness" or "binding strength"
Mathematica's 1000 - Level Precedence Table
Abbreviated Operators
This list includes all nondefined operators as of v8.0, about an increase of 60 more over v6.0. I include a few of a group of syntax operators that have Precedence = 670, such as Parentheses, Comma, and Subscript. These are which are referred to in the documentation as "structural operators."
abbreviatedOperators = {Operate, Through, Pi, I, Unset, Plus, N, Infinity, Tilde, Backtick, Level, Position, Alternatives, Repeated, RepeatedNull, Condition, Except, AddTo, PreIncrement, Increment, Decrement, PreDecrement, Map, MapAll, MapAt, MapThread, Apply, Factorial, Factorial2, Prefix, Postfix, Infix, MatchFix, Comma, Head, Part, PatternTest, Power, Function, Set, SetDelayed, Rule, RuleDelayed, TagSet, UpSet, Unset, Put, PutAppend, Append, PrependTo, AppendTo, Get, Overscript, Underscript, Subscript, Sum, Product, Coproduct, PartialD, DifferentialD, Integral, Cap, Cup, TimesBy, Replace, ReplaceAll, Colon, SemiColon, CompoundExpression, Therefore, Because, And, Or, Not, Element, ForAll, Exists, NotExists, Xor, Nand, Nor, SuchThat, Implies, RoundImplies, RightTee, LeftTee, DoubleRightTee, DoubleLeftTee, VerticalSeparator, Union, Intersection, Vee, Wedge, Backslash, Divide, PlusMinus, MinusPlus, CirclePlus, CircleMinus, Times, CircleTimes, CenterDot, Diamond, Star, NonCommutativeMultiply, Cross, Dot, D, Del, Square, SmallCircle, Integrate, Sqrt, Conjugate, Transpose, ConjugateTranspose, Derivative, StringJoin, Slot, SlotSequence, Out, In, Blank, BlankSequence, BlankNullSequence, Optional, Pattern, Default, MessageName, Piecewise, Symbol, String, Integer, Real, Complex, FullForm, Null, List, AngleBracket, Floor, Ceiling, BracketingBar, DoubleBracketingBar, Parentheses, Quote, DoubleQuote, Percent, SubtractFrom, DivideBy, Equal, Greater, Unequal, Less, LessEqual, SameQ, UnsameQ, Question, Underscore, Slash, FormBox, Hold, HoldPattern, "=*=", Conditioned, Distributed};
Length@abbreviatedOperators
165
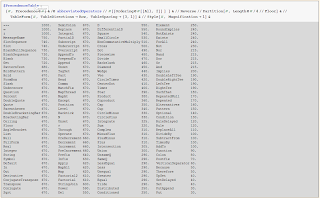
After defining the table of Abbreviated Operators, this code generates the first formatted table that you see at the top of this post, listing them in descending order of Precedence.
$PrecedenceTable = {#, Precedence@#} & /@abbreviatedOperators // #[[Ordering@#[[All, 2]] ] ] & //Reverse // Partition[#, Length@#/4 // Floor] & //TableForm[#, TableDirections -> Row, TableSpacing -> {3, 1}] & //Style[#, Magnification -> 1] &
And this code generates the second formatted table that you see at the top of the next post, listing Abbreviated Operators alphabetically.
$PrecedenceTable = {#, Precedence@#} &/@ abbreviatedOperators // #[[Ordering@#[[All, 1]] ] ] & //Partition[#, Length@#/4 // Floor] & //TableForm[#, TableDirections -> Row, TableSpacing -> {3, 1}] & //Style[#, Magnification -> 1] &
