A New Mathematica Programming Style, Part One

This is the presentation I gave at the Wolfram User Conference in 2007, updated for version 8. Part Two is here.

A New Mathematica Programming Style, Part One

Kris Carlson

Author, The Way of Mathematica (forthcoming)

An Historical Perspective on Computer Programming

"The computer revolution is a revolution in the way we think and in the way we express what we think. The essence of this change is the emergence of ... procedural epistemology--the study of the structure of knowledge from an imperative point of view, as opposed to the more declarative point of view taken by classical mathematical subjects. Mathematics provides a framework for dealing precisely with notions of 'what is.' Computation provides a framework for dealing precisely with notions of 'how to.'"

Harold Abelson and Gerald Jay Sussman, The Structure and Interpretation of Computer Programs

Origins of Geometry

Beginnings: Accurately surveying land boundaries

Destiny: Euclid's creation of the first axiomatic science

Origins of Computer Programming

Beginnings: Very abstract notions of computation by Church, Turing, Kleene and others

Destiny: The control of complex processes

The Main Challenges of Modern Science

Genetic Engineering

Taking control of the analog computer program immanent in DNA-RNA-protein

Artificial Intelligence

Reverse-engineering the agencies of intelligence created by evolution and creating new ones

Creating and initially controlling intelligences greater than our own

Nanotechnology

Programming at the atomic and molecular level to control materials

These challenges put the Abelson/Sussman thesis in perspective : It' s all about controlling complex processes

What about "A Theory of Everything?"

A misnomer. If created, which I doubt it will be, it would be nothing more than a theory of the currently known physical microcosm

Note that computer programming cannot be derived from it--but it can be derived from computer programming

Mathematica's Place in History

Mathematica is a scientific synthesis like those of Euclid, Spinoza, Newton, Locke, Lagrange, Hamilton, Darwin, Maxwell, Gibbs, Shannon, and others

"Everything is an expression"--a central unifying syntactic principle like energy in physics or bits in information theory

More Elements of the Mathematica Synthesis

General symbol manipulation program

Pattern matching engine

A variety of programming styles and devices

Axiomatization of lower-level functionality (Table, Map* family, Nest* family, etc.)

Interpret and compile modes

Interface/IDE\--the Front End Notebook

Plethora of built-in functions

Extension to all special functions via Mathematica Functions site

Extensive and growing graphics and visualization capabilities

Effectively unlimited notation synthesis

Equation solving

Numerical analysis/evaluation

Axiomatization of higher-level functionality (CellularAutomata, Manipulate, TuringMachine, etc.)

gridMathematica

Documentation Center

MathWorld

Presentation and documentation formats

webMathematica

Demonstrations site

Curated data/Data paclets

Incipient semantic net (WordData)

What is the goal of programming style?

Help manage ever-increasing complexity

Streamline the human-computer interface from both sides

A New Mathematica Programming Style

First principle: Replace all matchfix single argument function applications f [ arg ] with Prefix function applications f @ arg

Requires some knowledge of the 1000-level Precedence table

Second principle: Replace nested matchfix with Postfix + pure Function

Prefix Functional Syntax

Cleaner and more efficient than matchfix

Use prefix function application, @, for single-argument functions

Matchfix style:

f[ g[ h[ i [j] ] ] ]

Prefix style:

f @ g @ h @ i @ j

First two syntactical problems with list- or matchfix-based language

1. Humans have difficulty parsing deeply nested expressions (>3)
2. Humans are not regular expression parsers

Basic Benefits of Prefix style

Every pair of brackets we lose makes our expressions easier to read and understand

Every pair of brackets for which we don't have to type or move the cursor saves us time

A Prefix Style Example

Each @ tells us there is no complex nesting for that function, no options or arguments to look for, no brackets to match.

We can focus our attention on the functions that do use matchfix and identify their arguments and options.

There are fewer nested brackets to sort out.

Here's some code from Trott, The Mathematica Guide to Graphics, in matchfix and Prefix styles:

Show[GraphicsArray[

Block[{$DisplayFunction = Identity},

(* display absolute value of 2D Fourier transform *)

ListDensityPlot[Abs[Fourier[Table[1/#[i, j], {i, 256}, {j, 256}]]],

Mesh -> False, ColorFunction -> (Hue[0.8 #]&)]& /@

{GCD, LCM}]]]

Show@GraphicsArray@

Block[{$DisplayFunction = Identity},

(* display absolute value of 2D Fourier transform *)

ListDensityPlot[

Abs@Fourier@Table[1/#[i, j], {i, 256}, {j, 256}],

Mesh -> False, ColorFunction -> (Hue[0.8 #]&)]& /@

{GCD, LCM}]

More Prefix Style Examples

Basic Usages

One argument function definitions:

f[x_] := Sin[x]

f@x_ := Sin@x

One argument functions or assignments:

Log@100^100//N

2.11139*10^66

walk1D3@n_:= NestList[#+Random[Real,{-1,1}]&, Random[Real, {-1,1}],n];

walk1D3@10

{-0.206019, -0.914893, -0.951759, -1.04967, -0.299963, -0.8917, -0.147434, 0.764746, 1.57289, 1.40045, 2.13796}

list5 = Range@10;

Clear@list5;

Histogram@%

Histogram[Null]

Needs@"Combinatorica`"

Multiple one-argument function composition:

f@g@h@i@j@k

Sin[g[h[i[j[k]]]]]

First@Rest@Most@Range@10

Function definitions with lists as argument:

f@{a_, b_, c_}:= n@{a,b,c}

Precedence in Mathematica

The main objection to Prefix is that you have to know operator precedence

However this objection applies to all abbreviated operators (+, *, ^, [[ ]], { }, /@, etc.)

Mathematica is endowed with "a variety of special characters that greatly increase readability and elegance."

FORTRAN (FORmula TRANslation; early and primitive, but elegant), Mathematica (an advanced synthesis):

A conscious effort was made to provide a path of least action or smooth transduction from mathematical notation to code

Further, a significant feature of V6 is the addition of 100 undefined operators to facilitate creating user-defined notations

I submit that if you use Prefix, you will use it more often than the most common abbreviated operators

Precedence directs the order of abbreviated operators' operation

Precedence can be symbolized by parenthetical grouping, such as: a + (b ^ c) versus (a + b) ^ c

The Mathematica reference on precedence in 5.2 was Table A.2.7, now is in tutorial / InputSyntax: Operator Input Forms

It lists all abbreviated operators in tables of decreasing precedence

However, a superior reference can be generated from a little code

There exists an undocumented function, Precedence

Voila:

Precedence@Prefix

640.

It is not Listable, but it should be! Either reset Attributes to Listable or just Map it:

Precedence /@ {Prefix, Factorial}

{640., 610.}

What happened in the previous slide?

Prefix is a little "stickier" than Factorial==@ sticks to n more than ! does--and so we got (IntegerDigits@n)! instead of IntegerDigits[ n! ]

When faced with a few abbreviated operators, map Precedence onto them in the order they present in your expression

a + b * c ^ d - e

Precedence /@ {Plus, Times, Minus, Power}

{310., 400., 480., 590.}

Precedence mnemonics: Think of operator "stickiness" or "binding strength"

Mathematica's 1000 - Level Precedence Table

Abbreviated Operators

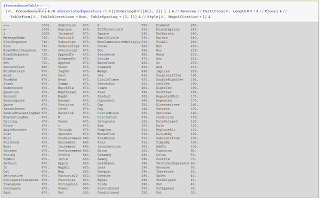
This list includes all nondefined operators as of v8.0, about an increase of 60 more over v6.0. I include a few of a group of syntax operators that have Precedence = 670, such as Parentheses, Comma, and Subscript. These are which are referred to in the documentation as "structural operators."

abbreviatedOperators = {Operate, Through, Pi, I, Unset, Plus, N, Infinity, Tilde, Backtick, Level, Position, Alternatives, Repeated, RepeatedNull, Condition, Except, AddTo, PreIncrement, Increment, Decrement, PreDecrement, Map, MapAll, MapAt, MapThread, Apply, Factorial, Factorial2, Prefix, Postfix, Infix, MatchFix, Comma, Head, Part, PatternTest, Power, Function, Set, SetDelayed, Rule, RuleDelayed, TagSet, UpSet, Unset, Put, PutAppend, Append, PrependTo, AppendTo, Get, Overscript, Underscript, Subscript, Sum, Product, Coproduct, PartialD, DifferentialD, Integral, Cap, Cup, TimesBy, Replace, ReplaceAll, Colon, SemiColon, CompoundExpression, Therefore, Because, And, Or, Not, Element, ForAll, Exists, NotExists, Xor, Nand, Nor, SuchThat, Implies, RoundImplies, RightTee, LeftTee, DoubleRightTee, DoubleLeftTee, VerticalSeparator, Union, Intersection, Vee, Wedge, Backslash, Divide, PlusMinus, MinusPlus, CirclePlus, CircleMinus, Times, CircleTimes, CenterDot, Diamond, Star, NonCommutativeMultiply, Cross, Dot, D, Del, Square, SmallCircle, Integrate, Sqrt, Conjugate, Transpose, ConjugateTranspose, Derivative, StringJoin, Slot, SlotSequence, Out, In, Blank, BlankSequence, BlankNullSequence, Optional, Pattern, Default, MessageName, Piecewise, Symbol, String, Integer, Real, Complex, FullForm, Null, List, AngleBracket, Floor, Ceiling, BracketingBar, DoubleBracketingBar, Parentheses, Quote, DoubleQuote, Percent, SubtractFrom, DivideBy, Equal, Greater, Unequal, Less, LessEqual, SameQ, UnsameQ, Question, Underscore, Slash, FormBox, Hold, HoldPattern, "=*=", Conditioned, Distributed};

Length@abbreviatedOperators

165

After defining the table of Abbreviated Operators, this code generates the first formatted table that you see at the top of this post, listing them in descending order of Precedence.

$PrecedenceTable = {#, Precedence@#} & /@abbreviatedOperators // #[[Ordering@#[[All, 2]] ] ] & //Reverse // Partition[#, Length@#/4 // Floor] & //TableForm[#, TableDirections -> Row, TableSpacing -> {3, 1}] & //Style[#, Magnification -> 1] &

And this code generates the second formatted table that you see at the top of the next post, listing Abbreviated Operators alphabetically.

$PrecedenceTable = {#, Precedence@#} &/@ abbreviatedOperators // #[[Ordering@#[[All, 1]] ] ] & //Partition[#, Length@#/4 // Floor] & //TableForm[#, TableDirections -> Row, TableSpacing -> {3, 1}] & //Style[#, Magnification -> 1] &